Labels
Posted by

Modified Bessel Function of the First Kind

DOWNLOAD Mathematica Notebook
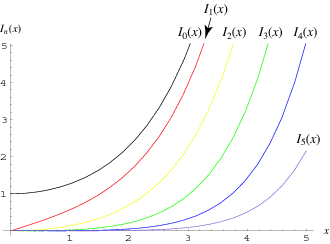
BesselI

A function I_n(x) which is one of the solutions to the modified Bessel differential equation and is closely related to the Bessel function of the first kind J_n(x). The above plot shows I_n(x) for n=1, 2, ..., 5. The modified Bessel function of the first kind is implemented in Mathematica as BesselI[nu, z].

The modified Bessel function of the first kind I_n(z) can be defined by the contour integral

I_n(z)=1/(2pii)∮e^((z/2)(t+1/t))t^(-n-1)dt,
(1)

where the contour encloses the origin and is traversed in a counterclockwise direction (Arfken 1985, p. 416).

In terms of J_n(x),

I_n(x)=i^(-n)J_n(ix)=e^(-npii/2)J_n(xe^(ipi/2)).
(2)

For a real number nu, the function can be computed using

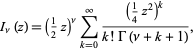I_nu(z)=(1/2z)^nusum_(k=0)^infty((1/4z^2)^k)/(k!Gamma(nu+k+1)),
(3)

where Gamma(z) is the gamma function. An integral formula is

I_nu(z)=1/piint_0^pie^(zcostheta)cos(nutheta)dtheta-(sin(nupi))/piint_0^inftye^(-zcosht-nut)dt,
(4)

which simplifies for nu an integer n to

I_n(z)=1/piint_0^pie^(zcostheta)cos(ntheta)dtheta
(5)

(Abramowitz and Stegun 1972, p. 376).

A derivative identity for expressing higher order modified Bessel functions in terms of I_0(x) is

I_n(x)=T_n(d/(dx))I_0(x),
(6)

where T_n(x) is a Chebyshev polynomial of the first kind.

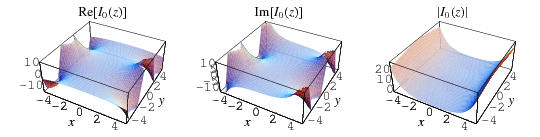
BesselI0ReIm
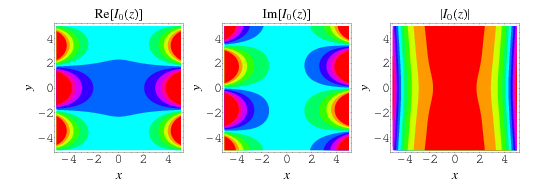
BesselI0Contours

The special case of n=0 gives I_0(z) as the series

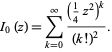I_0(z)=sum_(k=0)^infty((1/4z^2)^k)/((k!)^2).
(7)

SEE ALSO: Bessel Function of the First Kind, Continued Fraction Constant, Modified Bessel Function of the Second Kind, Weber's Formula

RELATED WOLFRAM SITES: http://functions.wolfram.com/BesselAiryStruveFunctions/BesselI/

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Modified Bessel Functions I and K." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 374-377, 1972.

Arfken, G. "Modified Bessel Functions, I_nu(x) and K_nu(x)." §11.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 234-245, 1992.

Spanier, J. and Oldham, K. B. "The Hyperbolic Bessel Functions I_0(x) and I_1(x)" and "The General Hyperbolic Bessel Function I_nu(x)." Chs. 49-50 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 479-487 and 489-497, 1987.

Labels:

Comments

Post a Comment

Popular Posts